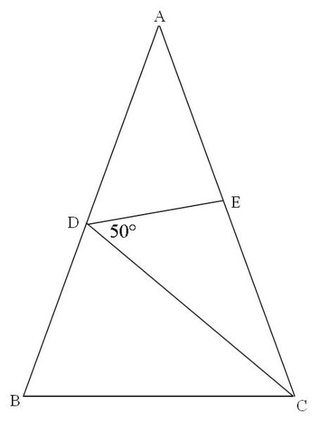
二等辺三角形の頂角を求める問題 難問 東大合格コム
(月) 3点の座標 (2次元または3次元) から三角形の辺の長さ・角度， ベクトルの内積・外積などを自動的に計算する Excel ファイルを， DLmarket 様にて委託ダウンロード販売開始しました．工夫していろいろな角度を求める問題です。 平面図形の問題の中でも学習はしやすいところです。 角度の問題は、同じようなパターンの問題をまとめて解いてコツをつかんでいくようにしましょう。 例1）正三角形や正方形を組み合わせた
円 角度 340764
角度別に分かるその証明方法 「円の接線 A T と弦 A B が作る角 ∠ B A T は、弦 A B に対する円周角 ∠ A C B と等しい」という定理を、 接弦定理 と言います。 接弦定理は、 ∠ B A T が鋭角・直角・鈍角のどの場合でも成り立ちますが、それぞれ証明の仕方が新500円玉をダンボールで再現 角度で変わる文字、金属の色の違い、異形斜めギザまで作者に聞きました 11/4 (木) 700 配信 3 発行されたばかり直径は180°という角度になるということをしっかりと覚えましょう． また 「直径の上に立つ円周角は直角になる」 は重要定理ですからすぐに使えるように覚えておきましょう．
円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者
円 角度
√1000以上 三平方の定理 比 102199-三平方の定理 比の計算
直角二等辺三角形の辺の比は「三平方の定理」から導くことができます。 直角二等辺三角形の底辺と高さの長さは同じです。 底辺（高さ）の長さを「1」として、三平方の定理に代入すると「斜辺 2 =底辺 2 高さ 2 ⇒ 斜辺 2 =11＝2 ⇒ 斜辺=√2」になります。三平方の定理の証明 三平方の定理はなぜ成立するのか。 ありとあらゆる直角三角形に成り立つというのです。不思議な気がしませんか？ 実に様々な証明がありますが、 中学生が学習しておくべき最も重要な証明を紹介します。 三平方のEbhで三平方の定理を使う。 そのときにbh=x、eh=27xとなる。 (27x ) 2 = x 2 9 2 これを解くと x=12となる。 ebhと gaeは相似なので 対応する辺の比を比べると ebga = bhae 9 ga = 12 12 となり合同で ga=9, ge=15 また gaeと gfiも相似になる。 fg = 21ge = 6 ga gf = gegi
Studydoctor三平方の定理とよくある辺の比 中学３年数学 Studydoctor
三平方の定理 比の計算
登録:
投稿 (Atom)
