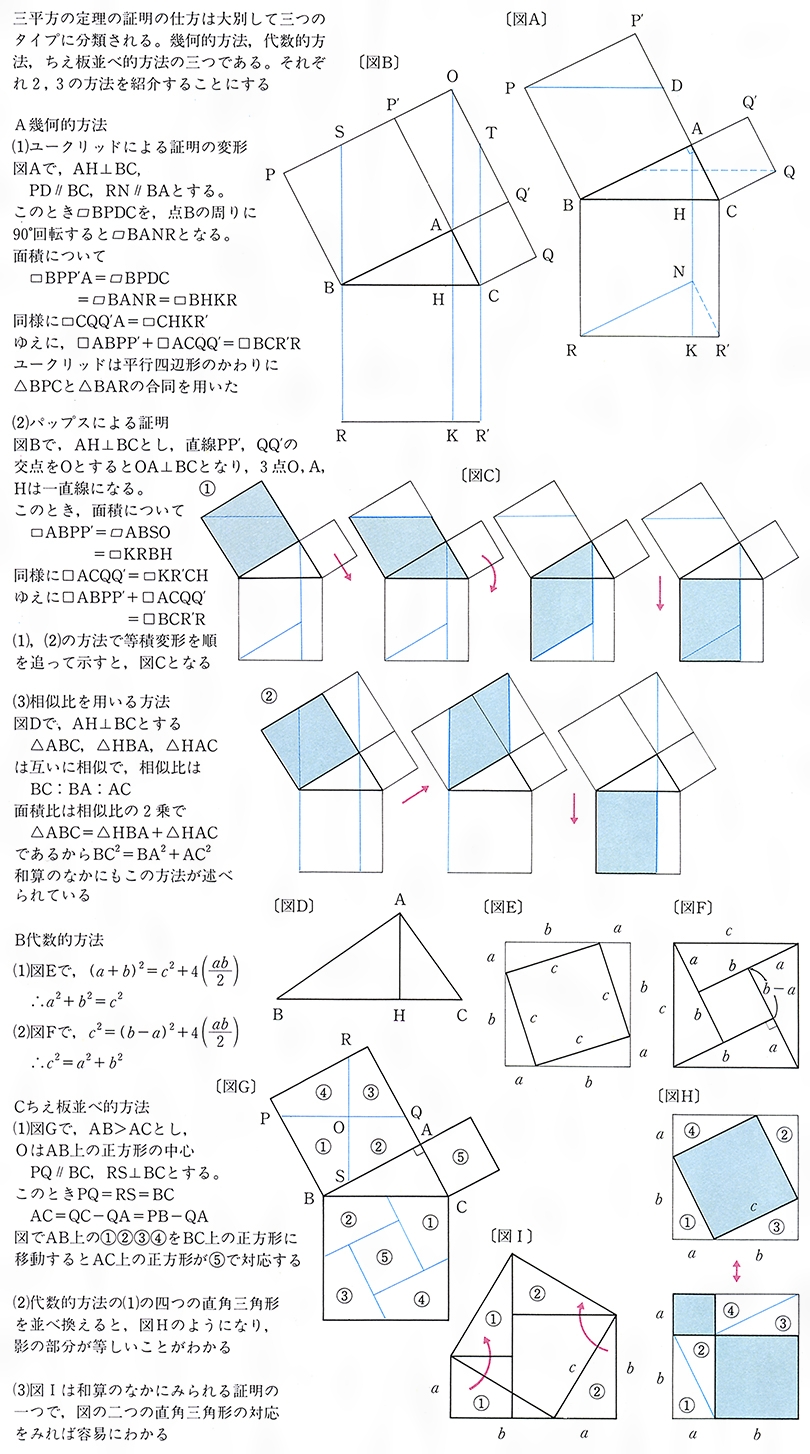
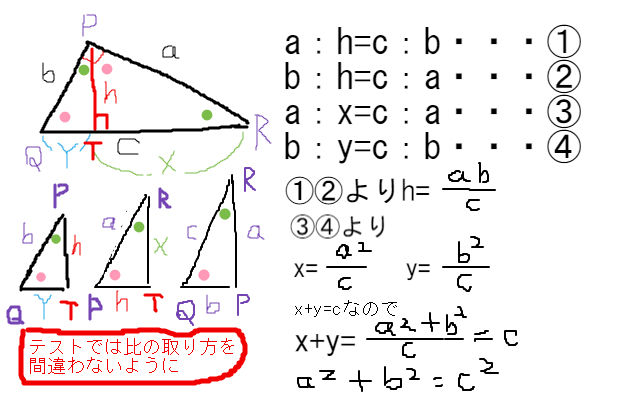
直角二等辺三角形の辺の比は「三平方の定理」から導くことができます。 直角二等辺三角形の底辺と高さの長さは同じです。 底辺(高さ)の長さを「1」として、三平方の定理に代入すると「斜辺 2 =底辺 2 高さ 2 ⇒ 斜辺 2 =11=2 ⇒ 斜辺=√2」になります。三平方の定理の証明 三平方の定理はなぜ成立するのか。 ありとあらゆる直角三角形に成り立つというのです。不思議な気がしませんか? 実に様々な証明がありますが、 中学生が学習しておくべき最も重要な証明を紹介します。 三平方のEbhで三平方の定理を使う。 そのときにbh=x、eh=27xとなる。 (27x ) 2 = x 2 9 2 これを解くと x=12となる。 ebhと gaeは相似なので 対応する辺の比を比べると ebga = bhae 9 ga = 12 12 となり合同で ga=9, ge=15 また gaeと gfiも相似になる。 fg = 21ge = 6 ga gf = gegi
Studydoctor三平方の定理とよくある辺の比 中学3年数学 Studydoctor
三平方の定理 比の計算
三平方の定理 比の計算-残り 1 辺を三平方の定理を使って求めると、 三平方の定理 1 2 x 2 = 2 2 これを解いて、 x = 3 よって、その辺の比は、 1 2 3 となります。 ② 45 °, 45 °, 90 ° POINT:正方形の半分 正方形の 1 辺の長さを①とすると、 1 辺は同じ長さなので①となります三平方の定理を使って、三角定規に使われている 2 つの代表的な直角三角形の辺の長さの比を求めてみましょう! この 2 つの三角形の一つは、3つの角が 45°、45°、90°の直角三角形です。



三平方の定理とは コトバンク
自然数比の三平方の定理といえば? それでは、自然数比で三平方の定理が成り立つ組合せはないのでしょうか。 皆さんが良く知っているものとして、345がありますね。 実はそれ以外でも、無数に存在します。その自然数の組をピタゴラス数といいます。空間図形と三平方の定理1 空間図形と三平方の定理2 立体の体積,表面積 立体の体積(入試問題) 立体の表面積展開図(入試問題) 1 右の図のように,AB=8cm,AD=7cm,AE=4cmの直方体ABCD-EFGHがある.頂点Aから,辺CD,GH,EF上をこの順に通って,頂点Bまで三角比 三平方の定理 直角三角形・三平方の定理 三平方の定理 c a b C A B 直角三角形においては a2 b2 = c2 ∠C = 90 となったとき余弦定理で cosC = 0 としたもの。 極めて重要な
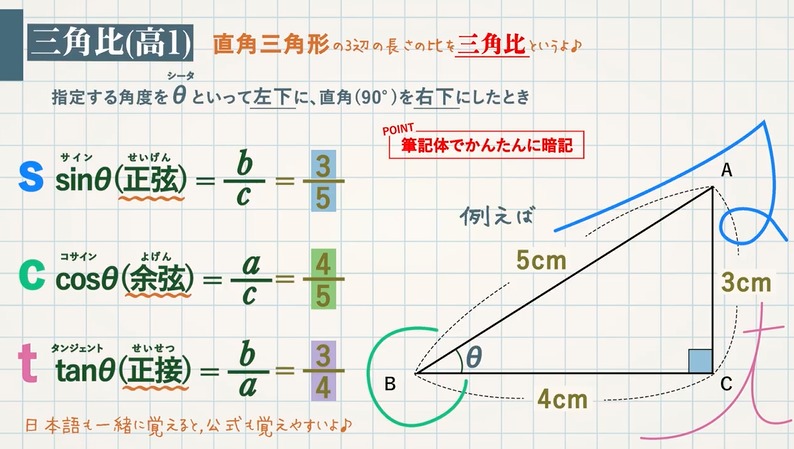
1/6 プロローグ(36秒) 2/6 今回のパパッと分かる問題(1分2秒) 3/6 ステップ1三平方の定理とは(3分54秒) 4/6 ステップ2 三平方の定理を使って三角比に慣れてきた人のために 上にあげた「サインとコサインを2乗して足すと1」という公式は、実は三平方の定理そのものです。 三角比とは、形を変えた三平方の定理といえます。 三平方の定理をもう少しわかりやすく、使いやすくするためにサイン ★無料の中学メルマガ講座★毎週、問題と動画講義をお届け! 勉強の習慣が身につく わかることが増えて楽しい 誰でも自由に学べる今すぐ無料
三平方の定理とは、直角三角形において3辺の長さの関係を表す公式のことをいいます。 直角と隣り合う2辺の長さをそれぞれ a 、 b 、直角の向かい側にある最も長い辺 (斜辺)の長さが c となる直角三角形があるとします。次の直角三角形の長さの比を に書き入れなさい。 /6点 1 45° 4 30° 45° 60° 45° x 7 NO 1 60° 2 4 x 60° 10 y 45° x x 三平方の定理 2 特別な三角形11 三平方の定理とは、 「不思議な直角三角形」の不思議さを説明したもの です。 直角三角形は、上の図のような形をしていて、内側の 3 つの角のうち、 1 つが 90 度になっています。




三平方の定理 覚えること 三角定規 苦手な数学を簡単に




三平方の定理の計算 この問題は絶対にできるようになろう 中学や高校の数学の計算問題
図を見てみよう。 「30°、60°、90°」 の直角三角形は、辺の比が 「1:2:√3」 になるよ。 覚えるだけで簡単に三平方の定理の計算問題が解けるよ。 覚えると便利!直角三角形の3つの比 それじゃあ早速、中学数学の問題でよく出てくる、 直角三角形の辺の比 を3つ紹介するよ。 比その1 「1 2 √3」 まず覚えておいておくべき直角三角形の辺の左の直角三角形が正三角形を半分にしたものです。 3 3 辺の比は暗記で、 21√3 2 1 3 です。 次に、右の直角三角形に三平方の定理を使うと、 最後の 1 1 辺の長さが求まります。 最後の 1 1 辺の長さを y y とすると y2 =102 y 2 8 2 = 10 2 y2 64 = 100 y 2 64



三平方の定理




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット
語呂合わせ 11 公式 1 原始ピタゴラス数~三平方の定理:直角三角形の三辺比 (1) 3 4 5 み_ よ_ ごちゃん_ さ_ し_ ごの直角余弦定理の図形的意味を考察する(1) 3 余弦定理や正弦定理を用いて、三角形の辺の長さや角の大きさを求める(2) 4 三角比を用いた三角形の面積公式を理解する(2) 5 正弦定理、余弦定理を空間図形の計量に応用する(2)(本時) 6初等幾何学におけるピタゴラスの定理(ピタゴラスのていり、英 Pythagorean theorem )は、直角三角形の3辺の長さの関係を表す。 斜辺の長さを c, 他の2辺の長さを a, b とすると、定理は = が成り立つという等式の形で述べられる 。 三平方の定理(さんへいほうのていり)、勾股弦の定理(こう



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




三角比 30 45 60 もう一度やり直しの算数 数学
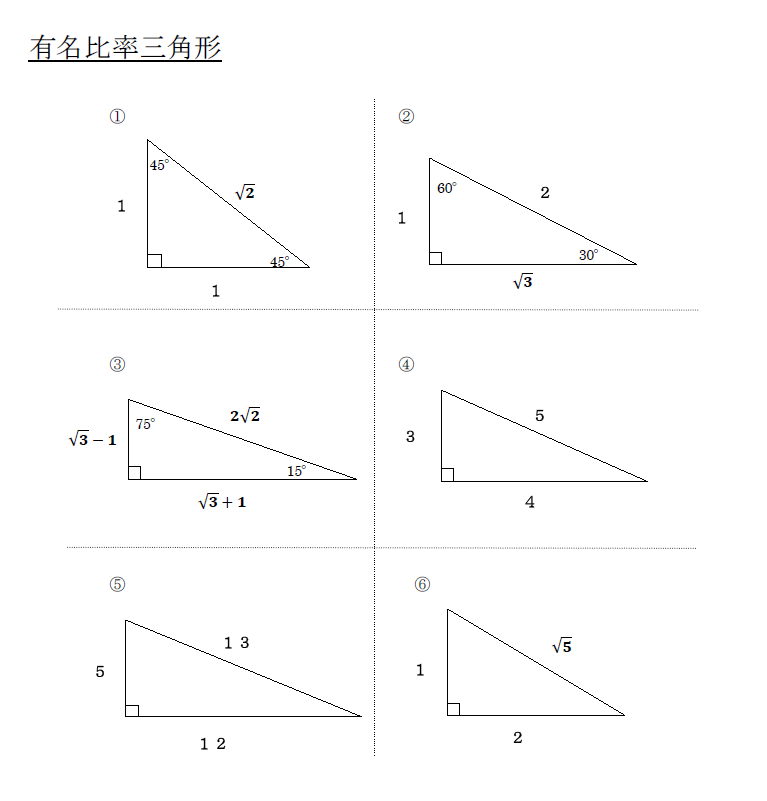
三平方の定理の証明⑪(相似を利用した証明1) 21年1月14日 中3数学 平面図形 中3数学 三平方の定理には数百もの証明方法があります。 今回は相似を利用した基本的な証明方法について紹介します。 目次 1 Ⅰ 三平方の定理とは 2 三平方の定理をもっと使いこなしていくために、下の \(\bf{4}\) パターンの直角三角形の角度と辺の比を覚えましょう。 これらの形を暗記すると、よりスピーディに計算できるようになり三平方の定理と黄金分割について(平成16年) 1定理の起源 三平方の定理は,古代メソポタミアがその起源とも考えられ, Carl B Boyerによると, 「ピタゴラスの定理は残存するエジプト文書にはいかなる形でも記されていない, メソ




21年度 都立入試の変更点 3 都立に入る



高校入試の出題分野より 三平方の定理と面積比 名古屋市北区の学習塾は思考力を育む 泰成スクール
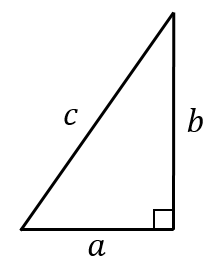
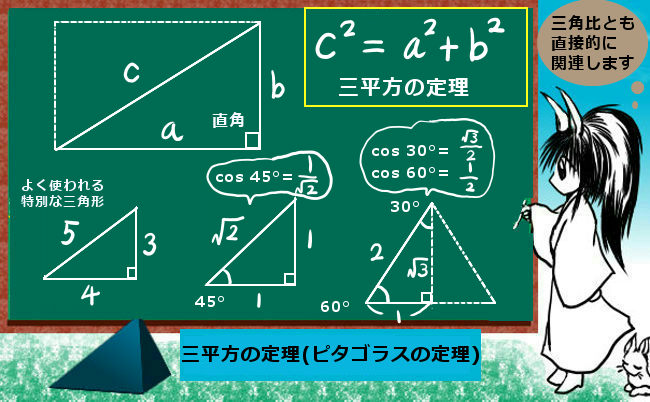
三平方の定理を使えば,直角三角形の2辺の長さが分かれば残りの1辺の長さが求められる. たとえば右図では, b , c が分かっていれば a が求められる.この問題を、三平方の定理を使って解きましょう。 「 直角三角形の斜辺の2乗は、他の2辺の2乗の和に等しい 」というのが三平方の定理でしたね。あれ? 三平方の定理ってさ 直角三角形のときに使える定理だったよね 斜辺の長さを2乗は、他の辺の2乗の和に等し




三平方の定理 覚えること 辺の長さ 苦手な数学を簡単に




三平方の定理について考える4 三角形の相似を使った証明方法 身勝手な主張
中3で学習する「三平方の定理」の中でも、これは応用問題です。例えば、こんな問題です。問題 上の図で、AB=、BC=21、CA=13です。 ABCの面積を求めなさい。まずは、三平方の定理までしか学習していない中3として、この問題をどう解くか考えてみま,セギ英数教室 角木優子三平方の定理 美樹 数学iで「図形と計量」という単元があります. 三角比の定義を習い,三角比を用いて長さや面積,体積を求めます. 要するに三角比なのですが, 三角比と計量の関係がよくわかりま




中3数学 3 4 5の直角三角形の辺の長さを求める3つの問題 Qikeru 学びを楽しくわかりやすく




3分でわかる 三平方の定理の公式と証明 利用と問題例 合格サプリ




三平方の定理の応用




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




三平方の定理の逆はなぜ成り立つ わかりやすく解説 遊ぶ数学




三平方の定理 特別な直角三角形の3辺の比 中学生からの勉強質問 数学 進研ゼミ中学講座
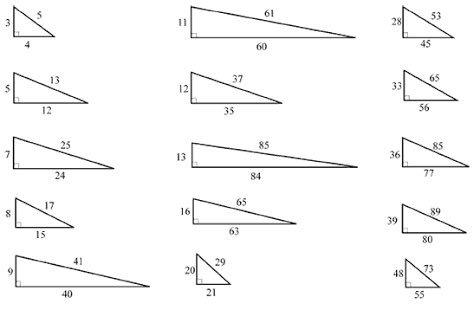



擔擔 予め覚えておくと便利な よく出る整数比になる直角三角形の例 別に知らなくても三平方の定理で出てくるわけだけど たとえば中上段の 11 2 60 2 3721だけど これが61の二乗であると知らなかったら 61が素数であることもあって が外せることに
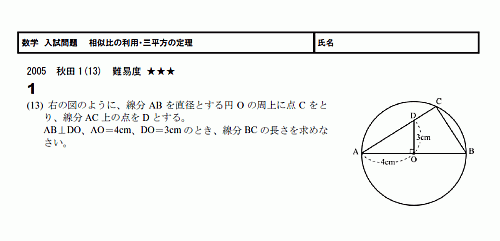



相似比の利用 三平方の定理 スタディーx




三平方の定理 覚えておきたい基本公式を解説 数スタ




中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット
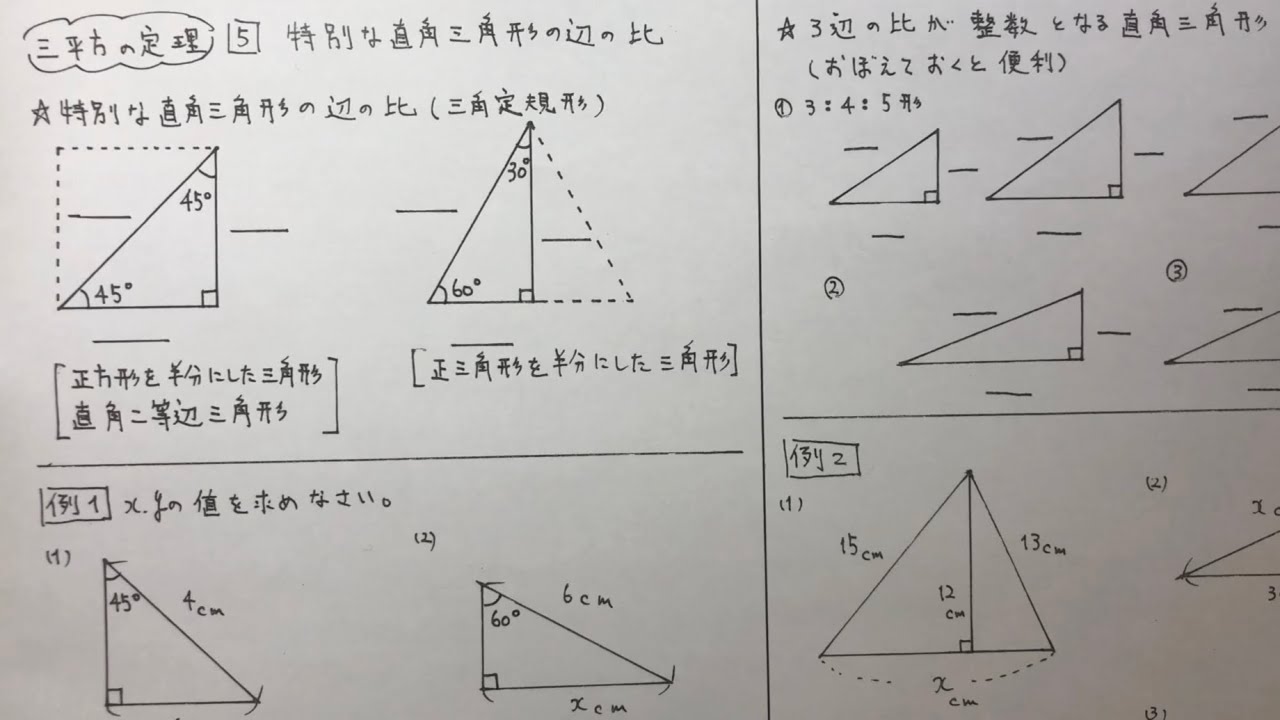



中3数学 三平方の定理5 特別な直角三角形の辺の比 Youtube




3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく



三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス




交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー




特別な直角三角形の辺の比 無料で使える中学学習プリント




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



Studydoctor特別な三角形と三平方の定理 中学3年数学 Studydoctor




三平方03 三平方の定理と比の計算 Youtube




三角比 高校物理の備忘録




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ
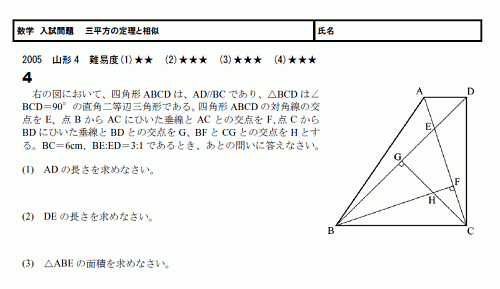



相似比の利用 三平方の定理 スタディーx




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




高校数学 第2余弦定理 三平方の定理の一般化 と第1余弦定理の証明と利用 受験の月
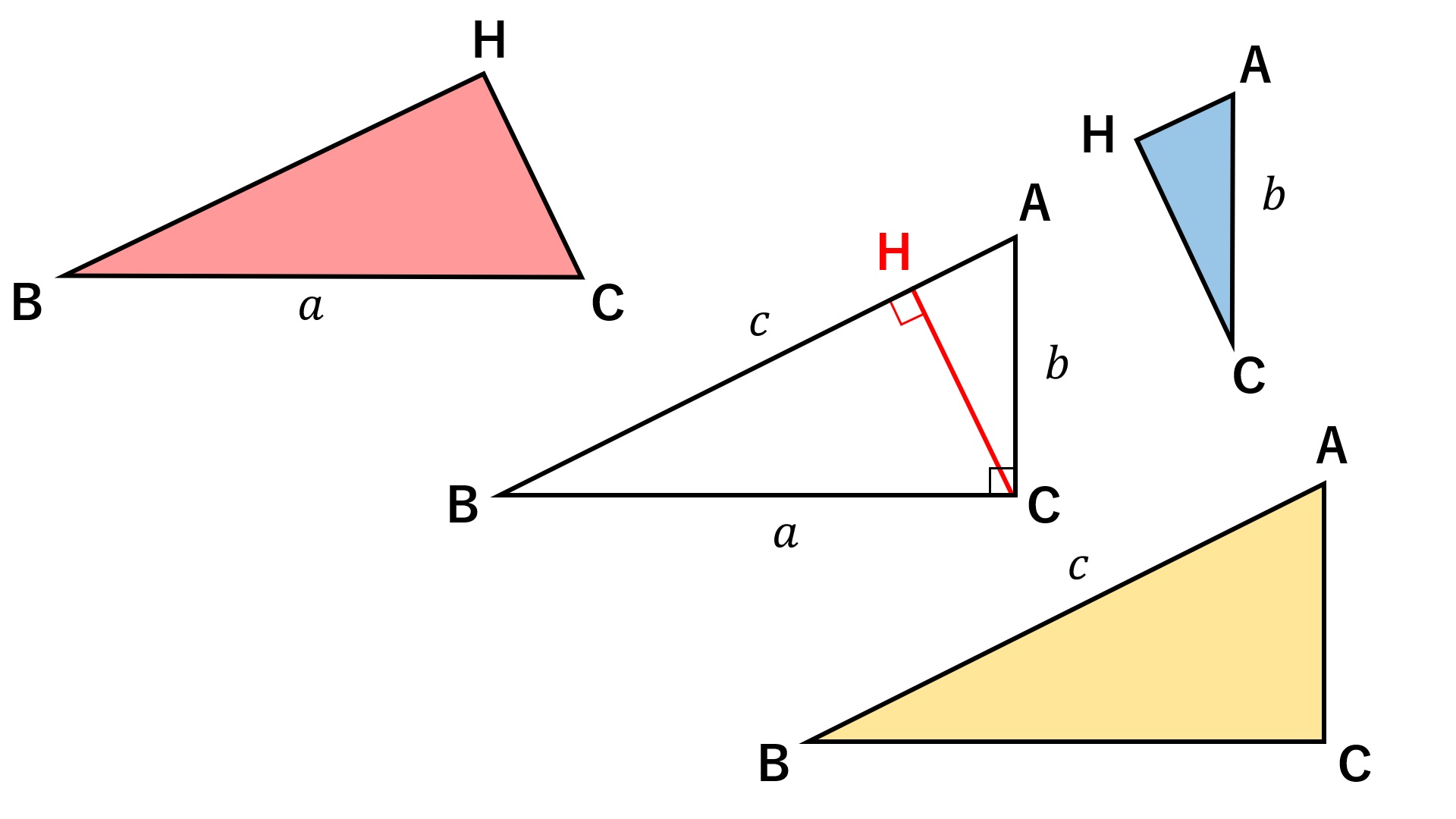



感銘を受けた数学 三平方の定理の美しき証明たち 数学 統計教室の和から株式会社




三角定規の直角三角形のときは 比の計算で簡単に求めよう 中学や高校の数学の計算問題



Studydoctor三平方の定理とよくある辺の比 中学3年数学 Studydoctor
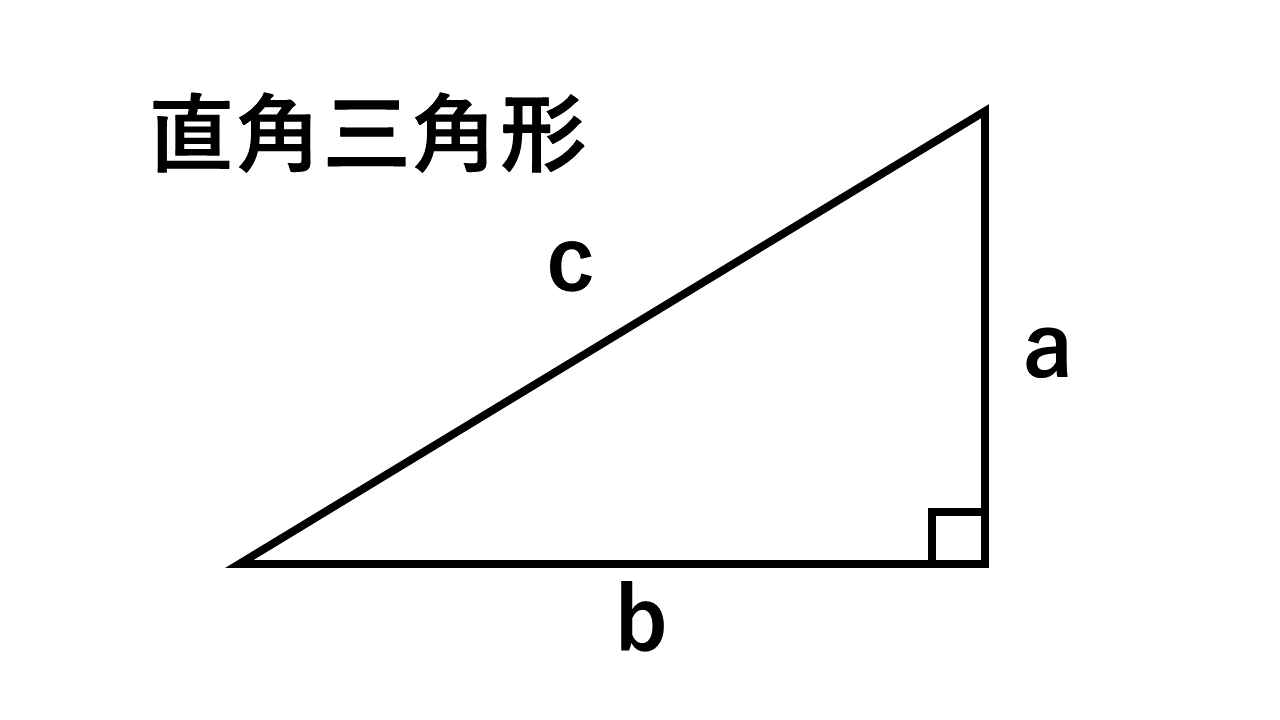



中学数学 直角三角形3 4 5以外に知ってる




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生




最高のピタゴラス の 定理 直角 三角形 ページを着色するだけ




余弦定理 は三平方の定理の進化版 余弦定理は2つある




三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube



三平方の定理




15 75 90 の三角形を考える 数学i フリー教材開発コミュニティ Ftext




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者
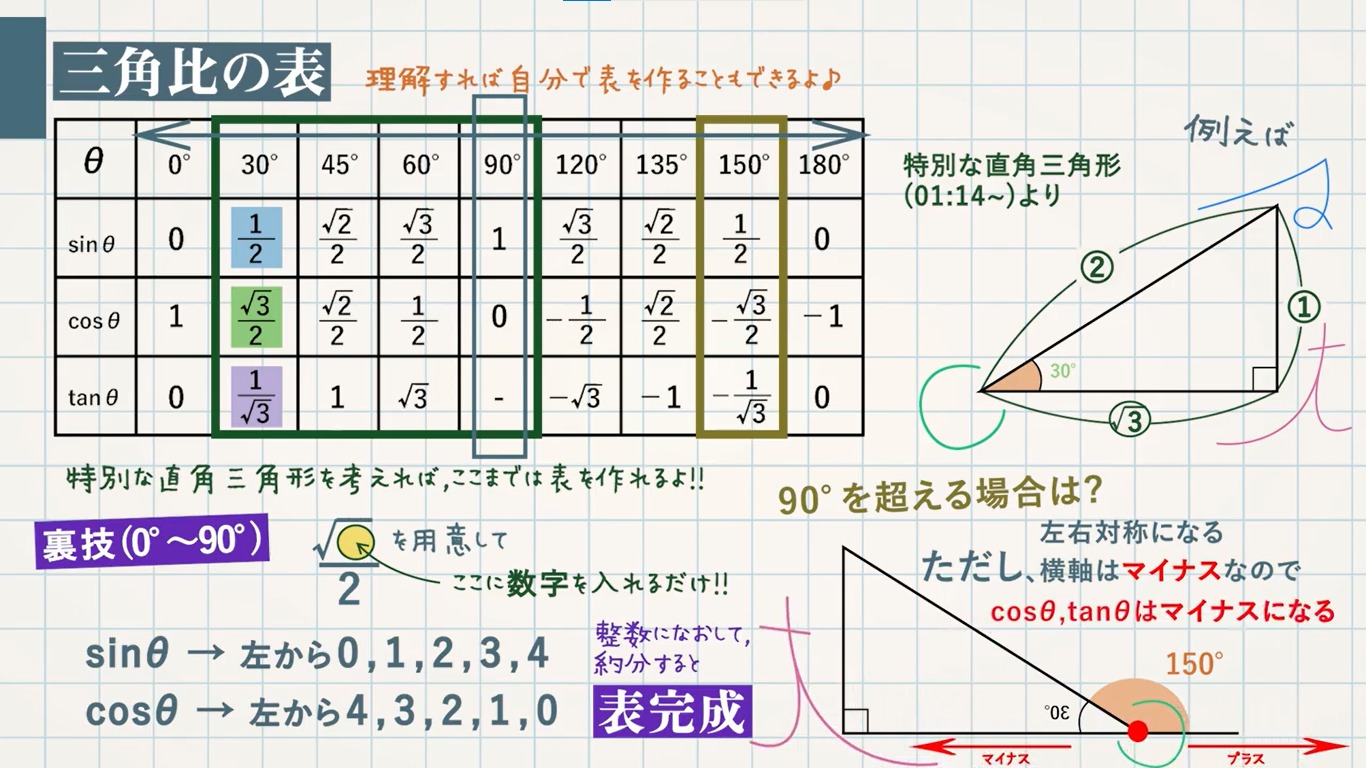



三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




三平方の定理 ピタゴラスの定理 とは 応用問題パターンまとめ10選 遊ぶ数学




無料 中3数学 基本解説 解答プリント 334 三平方の定理2 比の利用



1



1




数学 中3 61 三平方の定理 基本編 Youtube



p f1



中学数学の最後にして最大の壁 三平方の定理はこれで満点ゲット 高校入試徹底対策ガイド




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




三平方の定理とは コトバンク




中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su




中3数学 3 4 5の直角三角形の辺の長さを求める3つの問題 Qikeru 学びを楽しくわかりやすく




山と数学 そして英語 三平方の定理と三角形の面積 さらに三角比 ヘロンの公式



三角比三平方の定理 Sincostanとは結局何なんですか Yahoo 知恵袋




三平方の定理の証明と使い方



直角三角形で 3辺の比が整数になる例25個と作り方 具体例で学ぶ数学




高校数学 三平方の定理による三角関数の計算 1 映像授業のtry It トライイット




三平方の定理の利用 四角錐 円錐 チーム エン




三平方の定理の二等辺三角形の比がありますが それを使うにはその図形の角度が写真のよう Clear




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




ピタゴラスの定理と三角関数 たまには大学受験 灘校の教室 家庭教師 C O D Club




三平方の定理の証明と使い方




三角比6 三平方の定理の暗算 怜悧玲瓏 高校数学を天空から俯瞰する




数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



三平方の定理から円周率を計算してみる Yamav1 02bのブログ



三角形の内角30度 60度 90度のとき辺の比は1 2 Root3になる Yahoo 知恵袋




三平方の定理で解くと値は答えと同じなのに 同じ問題で三角比で解くと値と答えが違う事っ Clear




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ



1




中3数学 有名角と比 例題編 映像授業のtry It トライイット




交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー




三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく



図形問題解決のために知っておくべき三平方定理の証明方法 中学数学 理科 寺子屋塾の復習サイト




三平方の定理です 途中式含め教えてください Clear




特別な直角三角形の3辺の比 の問題が分からないんですけど やり方を教えてください Clear




三平方の定理 特別な直角三角形の3辺の比 中学数学 定期テスト対策サイト
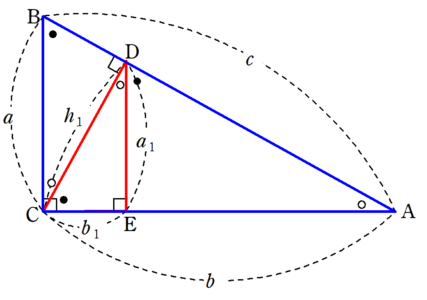



三平方の定理の証明 無限等比級数を利用した証明 Fukusukeの数学めも




三角比を考え方から理解する 有名角の三角比も説明




中3数学 有名角と比 例題編 映像授業のtry It トライイット
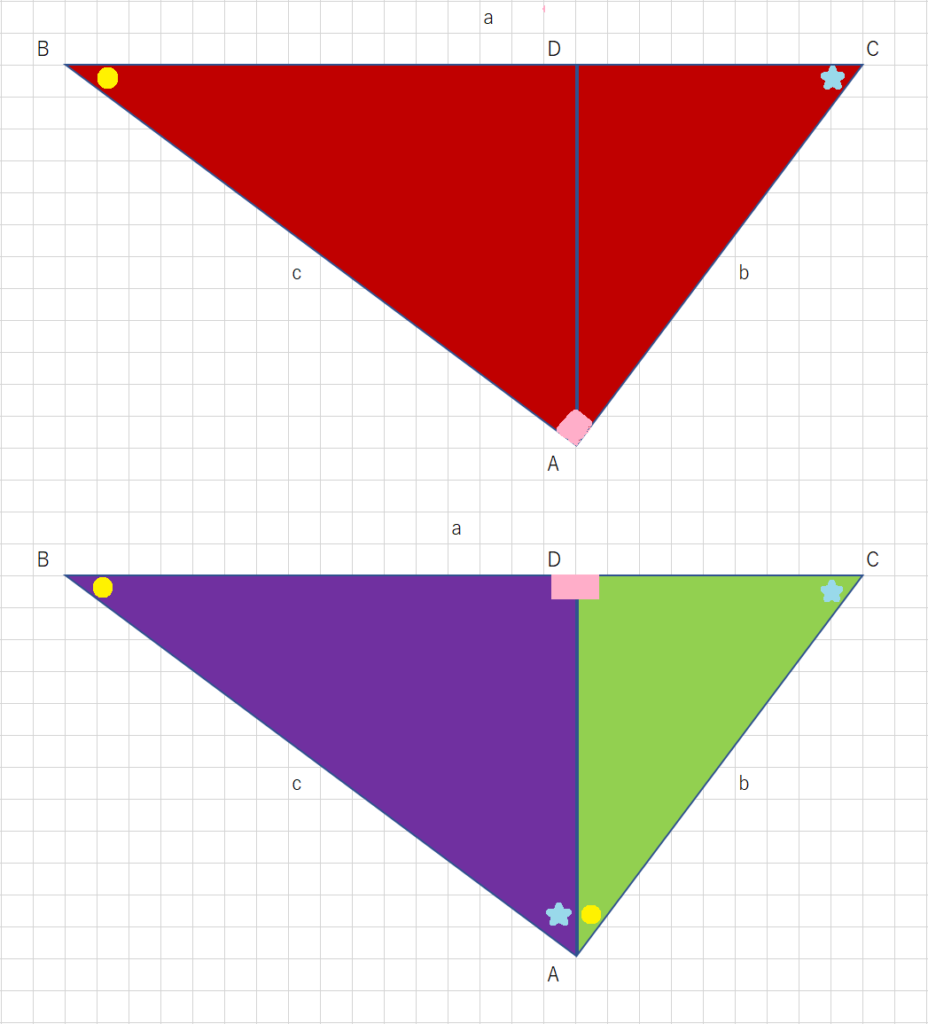



中学数学 直角三角形の三平方の定理とは ピタゴラス 平方根 の定理をexcelの図形で Curlpingの幸せblog



1



三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者



受験 定期試験 数学解き方集 裏技 解法 三平方の定理のテクニック 中学数学 高校数学




中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生



三平方の定理およびその逆 証明 理数系無料オンライン学習 Kori




三平方の定理で辺を求める Youtube




応用 15度の三角比 なかけんの数学ノート




三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学




三平方の定理 ピタゴラスの定理 の公式と計算方法 リョースケ大学




三平方の定理 ピタゴラスの定理 と三角比の導入 教遊者




三平方の定理とよくある辺の比 中学3年数学 Youtube




三平方の定理の証明と使い方



三平方の定理とは 証明や計算問題 角度と辺の比の一覧 受験辞典




三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ




高1 三角比 概論 余弦定理 三平方の定理 Sin8cos8tan8 Youtube




高校数 三角比 補足 15 75 について オンライン無料塾 ターンナップ Youtube



0 件のコメント:
コメントを投稿